- 2025. 나이트투어 (Ruby IV)
보드의 크기와 시작 위치가 주어질 때, 그 위치에서 시작하여 모든 칸을 한 번씩 밟는 나이트 투어가 존재한다면 그러한 경로를 아무거나 하나 출력하는 문제.
이 글에서는 이 문제의 기존에 알려지지 않았던 만점 해구성 풀이를 소개한다.
- 보드는 정사각형이며, 보드의 크기는 6 이상 666 이하
알려진 풀이
애초에 나이트 투어라는 문제가 수학에서 유명하고 역사가 깊은 문제이기 때문에, 여러 가지 알려진 풀이나 접근법이 존재한다. 그 중에서 해당 BOJ 문제의 정해로 알려진 것은 Warnsdorf’s rule이라는 휴리스틱을 사용하는 것이다. 해당 문제에서는 224/256점만 받으면 AC를 받을 수 있기 때문에, 이 방법을 적당히 잘 지지고 볶으면 AC 컷을 달성할 수 있다고 한다.
s,t-나이트 투어 해구성 풀이
해당 Wikipedia 글의 reference 중에는 s,t-나이트 투어, 즉 시작점과 끝점이 주어질 때 나이트 투어를 구성하는 문제를 푼 논문도 있다. 그 논문을 보게 되면 보드를 아주 복잡하게 쪼개고 수많은 하드코딩된 부분 보드들을 잘 이어붙여서 전체 투어를 구성한다. doju님의 게시판 요청 글에 언급된 “굉장히 많은 case study를 필요로 하는” 알고리즘이 이것이지 않을까 추측된다.
본인의 해구성 풀이
하지만 이 문제는 시작점만 주어져 있으므로, 위의 논문보다 훨씬 쉬운 접근이 있지 않을까라는 의문이 있었다. 그리고 며칠을 고민해 본 결과, 실제로 그러한 접근을 발견하는 데 성공했다.
이 풀이의 첫 번째 아이디어는 하나의 $2 \times 2$ 영역에 네 개의 나이트를 놓았을 때, 그 영역을 한 칸씩 상하좌우로 움직인 궤적을 네 개의 부분 투어로 나타낼 수 있다는 점이다. 그러한 영역을 편의상 ㅁ이라고 하자. 아래는 하나의 ㅁ을 위, 오른쪽, 아래, 왼쪽으로 한 칸 움직였을 때의 상황을 나타낸다.
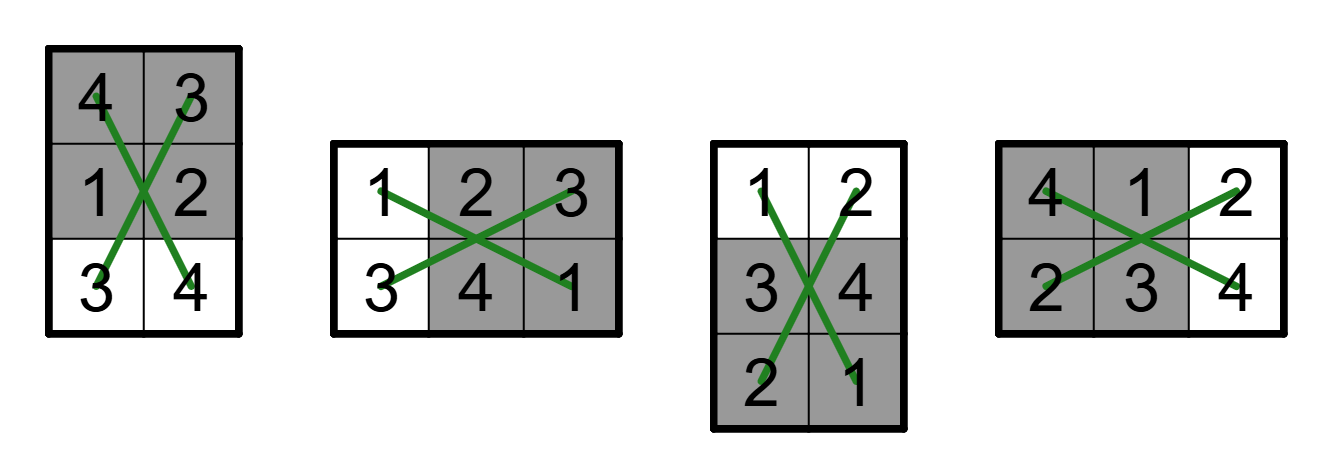
그림 1. ㅁ의 단위 이동
이제 이러한 ㅁ의 경로를 이용하여 판을 재귀적으로 좁힌다. 이때 남은 판은 정사각형을 유지하는 것이 나중에 base case를 줄이는 데에 도움이 되며, 그 경로의 양끝점은 계속해서 남은 영역과 이웃한 자리에 있어야 계속 확장이 된다. 그리고 ㅁ은 주어진 시작점을 밟으면 안된다는 것도 고려하여야 한다.
시작점을 대칭에 의해 왼쪽 위 사분면의 주 대각선 또는 그 위쪽 영역으로 한정한다. 나중에 출력할 때는 완성된 투어의 모든 좌표를 역순으로 변환해서 출력하면 된다. 또한 ㅁ 경로의 두 끝점의 위치를 $n \times n$ 영역 바로 아래에 “왼쪽 정렬"한 위치로 정했다. 그러면 $n \ge 9$에 대해 다음의 3가지 방법 중 하나를 사용하여 크기 $n-4$의 보드로 좁힐 수 있다. 본인의 코드에서는 시작점의 x, y가 모두 2 (0-based) 이상이면 1번, x가 4 이상이면 2번, 아니면 3번을 사용하였다.
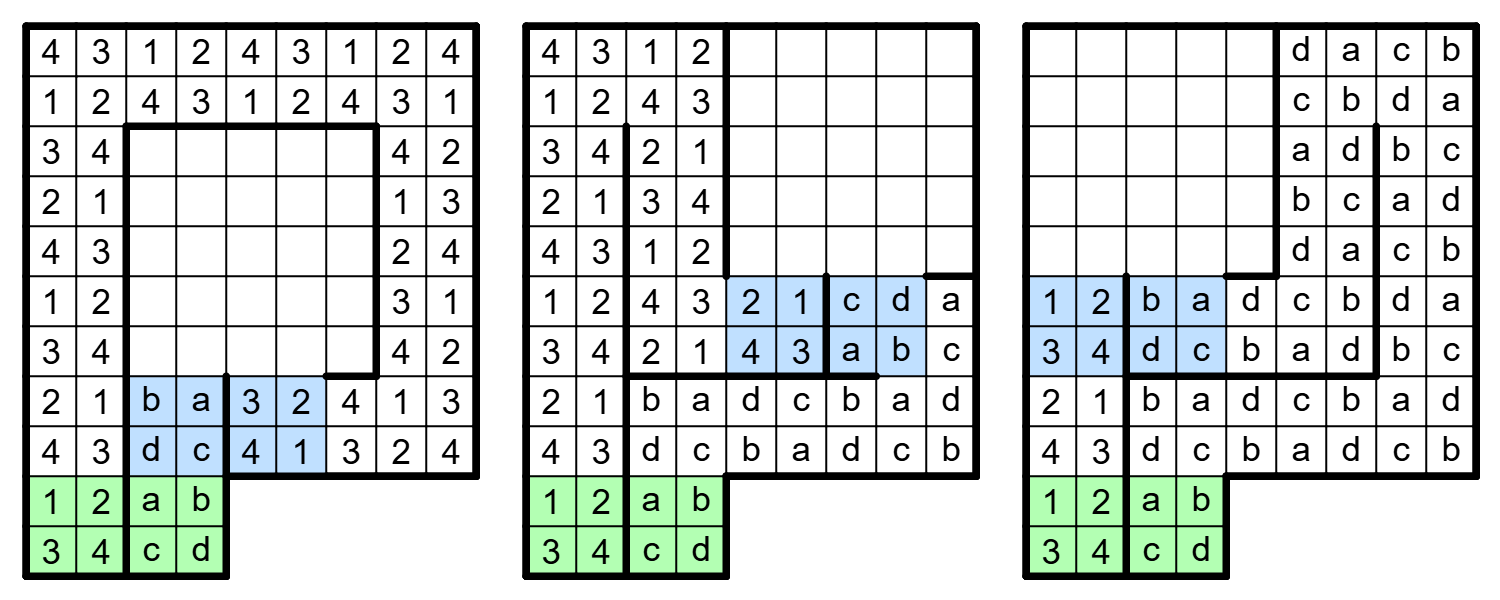
그림 2. ㅁ 경로의 확장을 통한 정사각형 영역의 축소
맨 처음의 경우 초록색 칸은 존재하지 않지만, 초록색에서 두 번 위로 이동한 위치에 양쪽 ㅁ을 위치시키고 그 둘을 두 개의 X자로 연결한 상태로 위 알고리즘을 진행하면 된다. 이렇게 하면 최종적으로 크기 5 이상 8 이하의 격자 영역과 하나의 ㅁ 경로가 남게 된다.
그런데 이렇게 보드를 좁히는 방법을 구현하였을 때, ㅁ 경로 위의 4개의 띠의 양 끝점은 사실상 아무렇게나 바뀔 수 있다. (사실 ㅁ이 총 짝수 번 이동하므로 항상 even permutation이 만들어지기는 하나, 이는 풀이에 별로 도움이 되지 않는다.) 그러면 이들의 12가지 연결 상태와 남은 영역에서 가능한 모든 시작 위치의 조합에 대해 투어를 하드코딩해야 하는 걸까?
다행히도 아니다. Permutation의 특성에 의해, 양끝 ㅁ을 잇는 두 개의 X자를 그리면 1개 이상 4개 이하의 닫힌 부분 나이트 투어가 만들어진다. 이제 원하는 시작점에서 시작하는 적절한 $n \times n$ ($5 \le n \le 8$) 나이트 투어를 그린 다음 다음과 같이 적당한 초록색 연결 쌍을 제거하고 빨간색 연결 쌍을 추가하면 하나의 연결된 나이트 투어가 만들어진다! 대신에, 작은 나이트 투어는 각 그림의 위쪽 초록색 선에 해당하는 4개의 선을 반드시 포함해야 한다는 제한 조건이 추가된다.
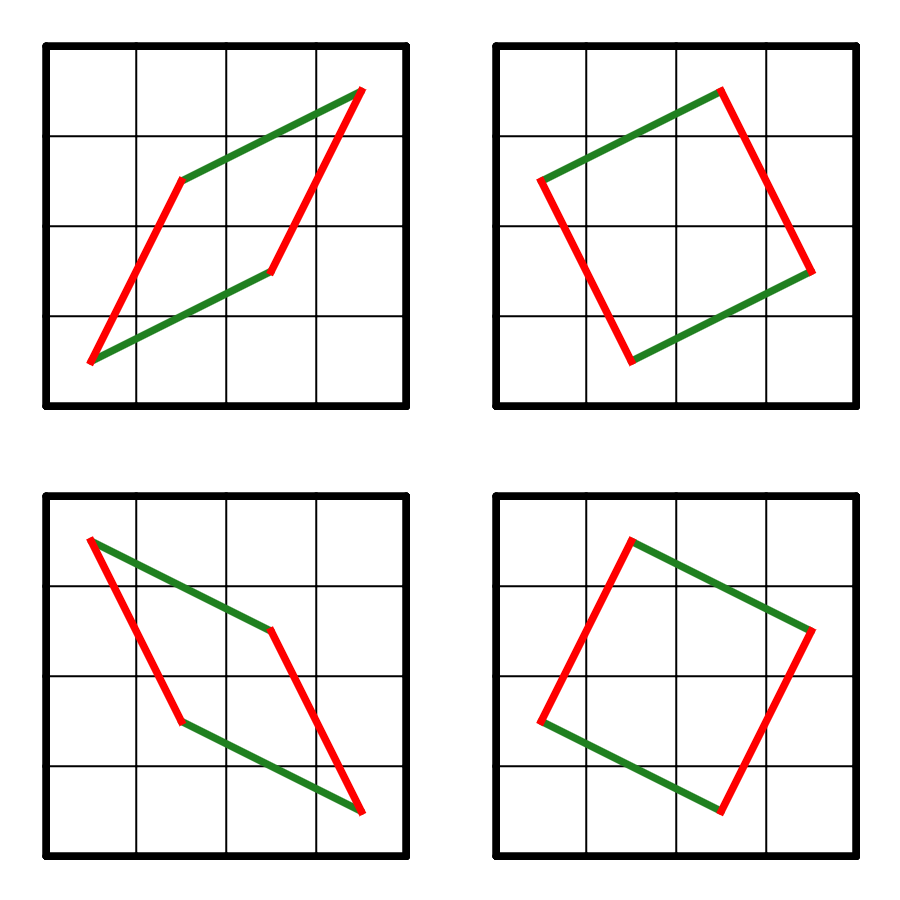
그림 3. 투어를 하나로 연결하기 위한 이동의 쌍들
이 시점에서 가능한 시작점의 개수는 $5 \times 5$에서 5개, $6 \times 6$에서 6개, $7 \times 7$에서 6개, $8 \times 8$에서 10개가 있다. $5 \times 5$의 나이트 투어는 잘 관찰하면 항상 한쪽 끝점이 꼭짓점에 있어야 함을 알 수 있고, $6 \times 6$과 $8 \times 8$은 닫힌 투어를 만든 다음 원하는 곳을 끊으면 된다. $7 \times 7$의 6개 시작점은 3쌍으로 짝지어 각각의 쌍을 양 끝점으로 하는 투어를 하나씩 만들면 3개의 투어로 해결할 수 있다. 위 조건을 충족하면서 하드코딩할 투어의 개수를 최소화(9개)하는 방법이 실제로 존재하며, 본인의 코드에서 사용한 9개의 투어는 다음과 같다.
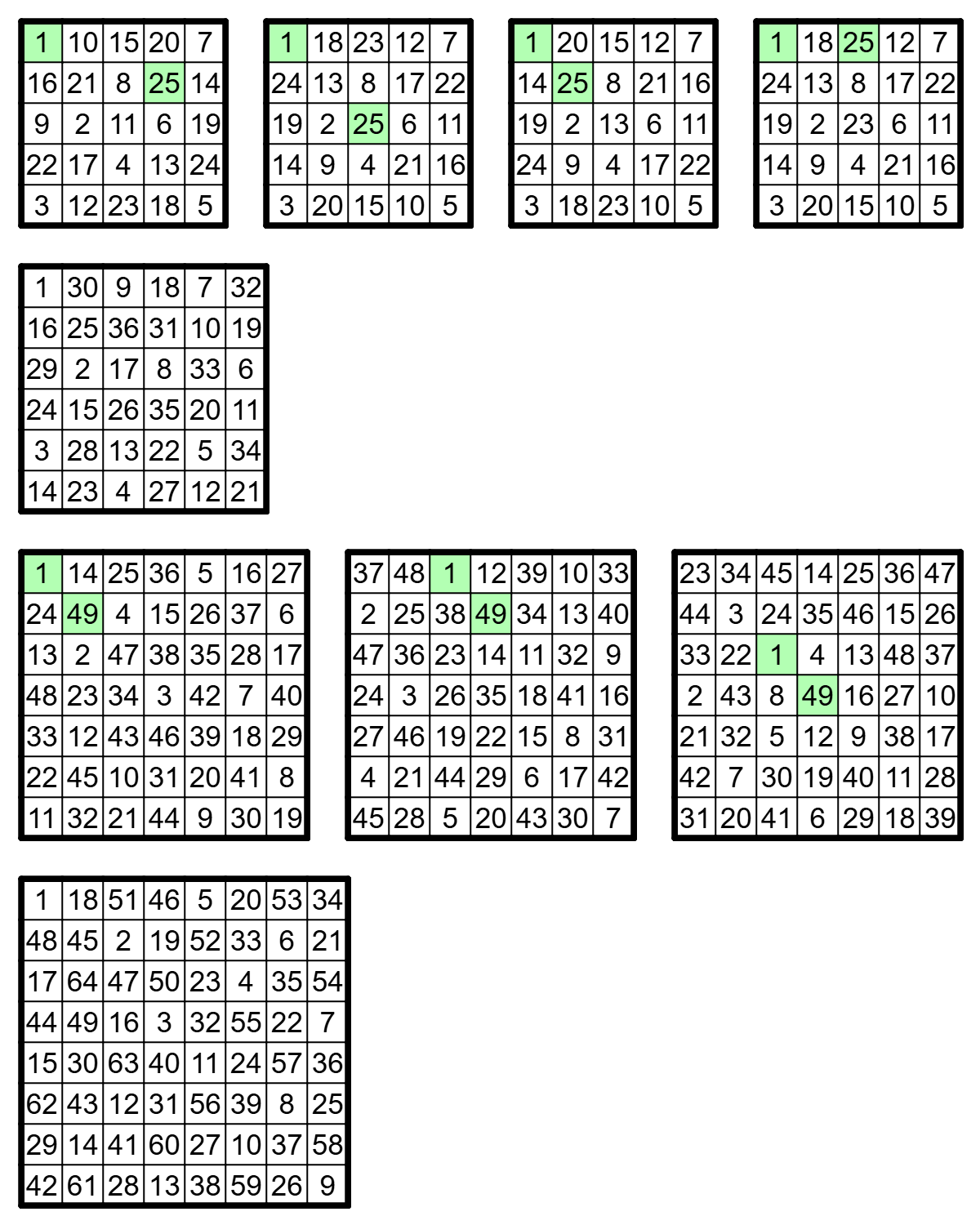
그림 4. Base case 투어의 목록